１．試験計画
　よく言われることであるが、品質特性を評価するための実験も信頼性を評価するための試験も、目的に沿ったデータを得るには準備段階での綿密な計画が不可欠である。理論編の2項「信頼性評価と母集団」に述べてあるように、信頼性データにおける母集団の範囲は、製品（試料）、動作条件、環境条件、故障モードなど多岐に及び、信頼性試験では母集団の範囲を特定することが特に重要になる。信頼性試験の計画書には、以下の項目が必要事項となる。
1)試験概要
2)試験試料
　信頼性試験では二つの壁（数と時間）があるため、同一製品の全シリーズを試験することは事実上不可能である。従って設計原理が同じと考えられるシリーズについては、一つの機種で代表してもよい。但し同一製品の全シリーズを一つに代表できるとは限らず、設計原理に応じて複数の機種を実施しなければならない場合もあり、何れが代表できるかについては担当製品のエンジニアが、固有技術の観点から決定する必要がある。
3)動作条件
　特別な条件がない「真っ当な寿命」を論ずる範囲では、製品仕様を代表する一般的な条件でよい。勿論製品業界内で検討された値（例えば規格で取り決められた条件）があれば、それが推奨される。場合により信頼性データを提供する顧客と取り決める必要がある。
4)モニタリング（特性項目、測定間隔）
　故障モードを検出するための特性値になり、一般的には一つの故障モードに対して一つの特性値が適用される。但し信頼性試験では、試験を継続したまま製品の特性値を連続データとして取得することは困難な場合が多く、一定期間毎に試験装置を停止させモニタリングすることになる。間欠データでは前回測定タイミングではOKであったが、今回の測定タイミングではNGということになり、故障に至った正確な時間は捉えることはできない。コスト（モニタリング工数）削減を重視して測定間隔を空け過ぎると、順序統計量としてのばらつきに影響を与える可能性がある。
5)故障モード
　試験する製品の摩耗系故障を的確に捉える観点から、故障モードを予め決定しておく必要がある。万一想定した故障モード以外の故障が発生した場合は、それらを同一の母集団として評価すべきか、若しくは異なる母集団として評価すべきかを検討する必要がある。
6)故障判断基準
　モニタリング特性が何れの値に至ったら故障と判断するかの基準であるが、これが意外と簡単ではない。製品の出荷検査規格が適用される場合があるが、この値は製品仕様を保証する為の値であり一般的にはかなり厳しい値になるため、摩耗系故障を捉える観点からは必ずしも適正とはいえない。製品業界内で検討された値（例えば公的規格で取り決めた値）があればそれが推奨されるが、ない場合は顧客フィールドにおける特性値の劣化がどの程度まで許容されるかなどで別途検討する必要があり、場合によっては信頼性データを提供する顧客と取り決める必要もある。
7)取得データの分析
　試験終了後若しくは中間報告時などにおける、データの分析方法を明確にする。摩耗系故障を観点とする場合は概ね以下の通りである。
　ワイブル解析による故障分布の推定（形状Par,、尺度Par.）
　信頼性特性値（B₁₀ライフ）の推定（点推定値と95%FM信頼下限値）

２．データ解析
2.1完全データの解析（グラフィック解析）
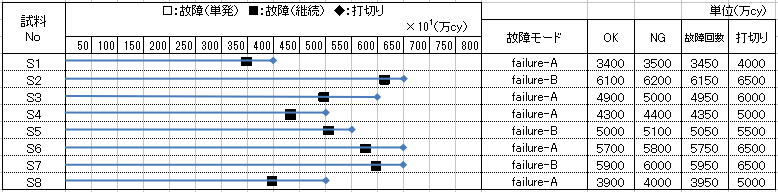
　信頼性試験を実施し、以下の信頼性データ（故障時間線図）が得られたものとしよう。試料数は8個で全数故障に至っており、完全データによる解析となる。信頼性解析をする上で故障時間線図を作成することは必ずしも必要ではないが、故障モード、故障特性値、故障時間（前回OK時間、今回NG時間）などを一覧として纏め、信頼性データを決定した過程を明確にすることは、解析確度の向上に繋がるだけでなく、データが母集団を代表しているかなどを検討する上で必要な情報にもなる。
　　3450,3950,4350,4950,5050,5750,5950,6150　(万回)
　　　　　　　　　　　　　　　　　　　　（故障時間線図）
　
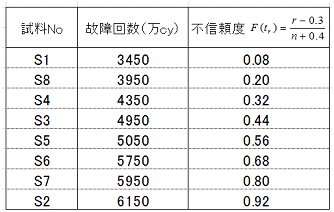
　1)不信頼度の推定
　各故障時間（回数）における不信頼度F(t_i)を推定する。理論編に示したようにデータの種類により幾つかの方法が考案されているが、我々が扱うデータ（完全データ、定数又は定時打ち切りデータ）は、基本的にメディアンランク法で推定しても構わない。各試料の故障時間（回数）を昇順に並べ替え、メディアンランク回帰法の式により不信頼度を求めると、以下表のように求まる。
　
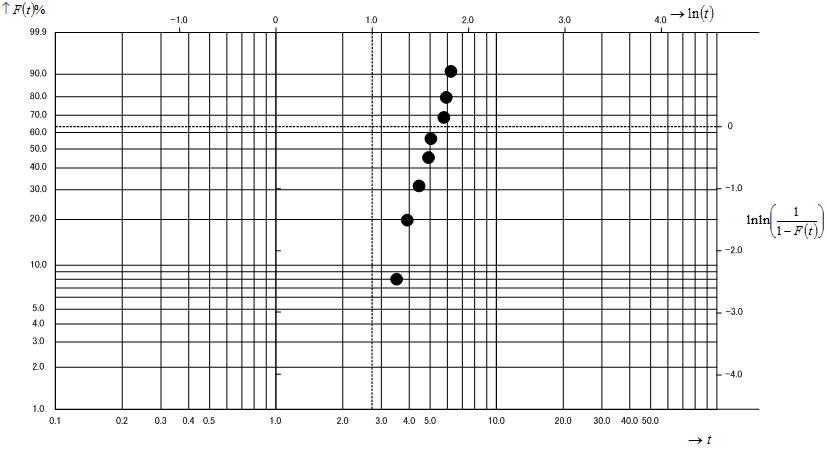
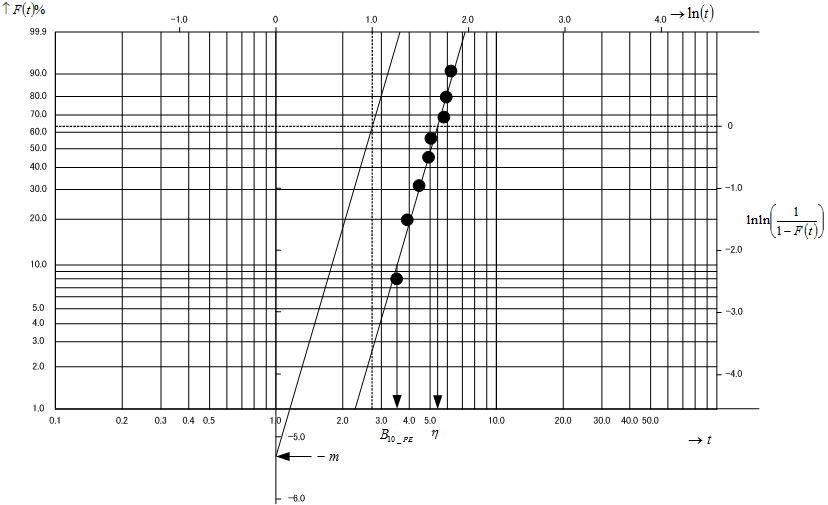
　2)データのプロット
　ワイブルチャートに計算により求めた不信頼度をプロットする。X軸には故障した時間を取るがプロット範囲がチャートの中心付近になるように、故障回数の値を適当な10の累乗で割り桁を圧縮する。故障回数（時間）を10³で圧縮し、対応する不信頼度の値をプロットすると以下のようにプロットされる。
　
　3)最適（回帰）直線を引く
　これは統計解析における回帰分析と全く同様で、プロット点を代表する直線を引くものである。厳密には最小二乗法を用いて計算することになるが、目で見た感じで引いても解析結果には殆ど影響はない。
　4)母数（形状Par.,尺度Par.）の推定
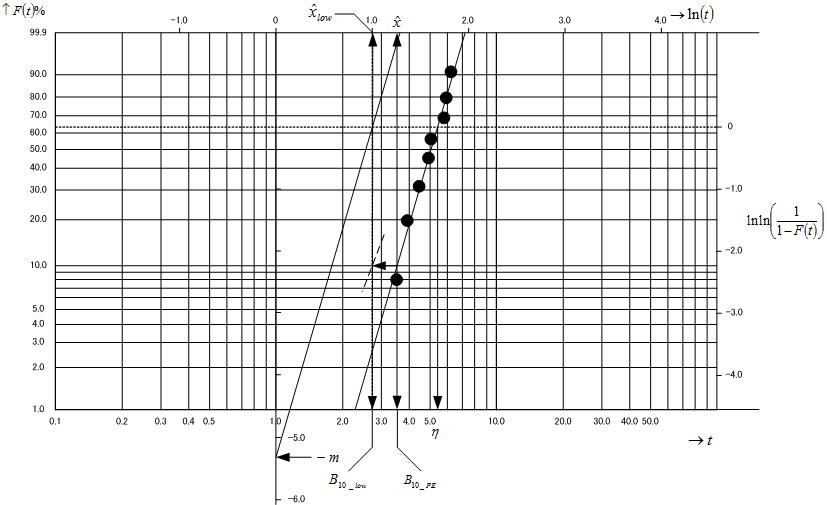
　最適直線をm 推定点（1,0）まで平行移動させ、その直線とln(t)=0の交点からY軸の値を読み取ると形状パラメータ（-m）が得られる。次に回帰直線とF(t)=63%の交点からX軸の値を読み取ると、尺度パラメータ（η）の値が得られる。
　5)信頼性特性値（B₁₀ライフの点推定値）の推定
　回帰直線とF(t)=10%の交点からX軸の値を読み取ると、B₁₀ライフの点推定値（B_{10_PE}）が得られる。グラフィック解析における各読み取り値は概ね以下のようである。
　　形状パラメータ：m =5.3
　　尺度パラメータ：η=5.3×10³　万cy
　　信頼性特性値（B₁₀ライフの点推定値）：B_{10_PE}=3.4×10³　万cy

　
　以上示した通りグラフィック解析では、チャートさえあれば手計算で故障分布を推定することができ、その推定精度も顧客が十分に満足できるレベルといえる。但し理論編に示したFM信頼限界は、別途ツール（数値解析）を用いて計算する必要がある。
2.2数値計算による検証例
　1)故障分布の推定
　2.1と同様のデータが得られた際の数値計算による解析値と、グラフィック解析における値と照合してみよう。最小二乗法によるパラメータを計算するには、ワイブルチャートの直線軸における（ｘ_ｉ，ｙ_ｉ）を求め、更にパラメータを計算するための各値を求める。
　
　

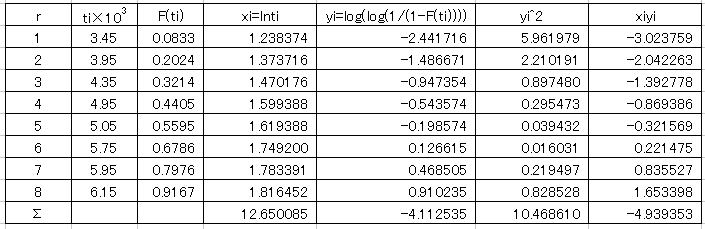
　理論編における形状Par,と尺度Par.の計算式により以下のように求めることができ、グラフィック解析でもほぼ近似の値が得られていることが分かる。　
　
　

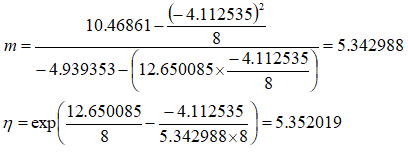
　2)FM信頼限界
　理論編で述べたようにFM信頼限界は時間と信頼度の二つのタイプがあるが、我々が興味があるのは時間の信頼限界である。さてFM信頼限界の論理展開は、私を含め一般的なエンジニアの出る幕ではないが、このようにすれば求められると先人の方々が証明されているので、我々はそれに従って計算するだけである。理論編に従って先ず形状Par.（m）と尺度Par.（η）の分散及び共分散を求めるため行列内の総和項を計算すると、以下の計算結果が得られる。
　
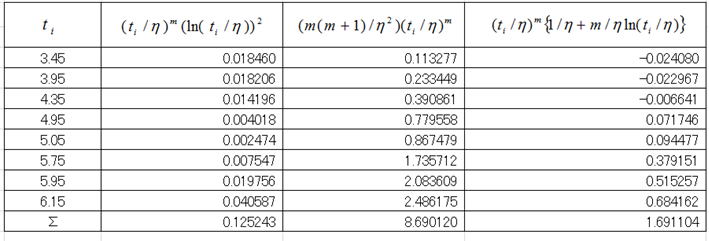
　これより各行列要素（I₁₁～I₂₂）を計算すると以下のようになる。従ってフィッシャー情報行列は最後の行列式として得られる。
　　　　
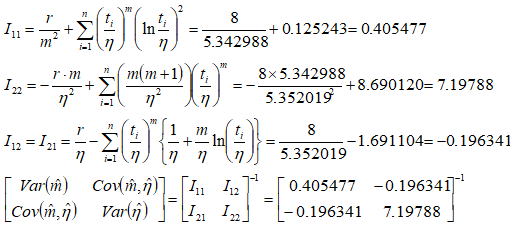
　逆行列の一般公式よりフィッシャー情報行列の各要素を計算すると、各分散及共分散は以下のように計算できる。
　　　
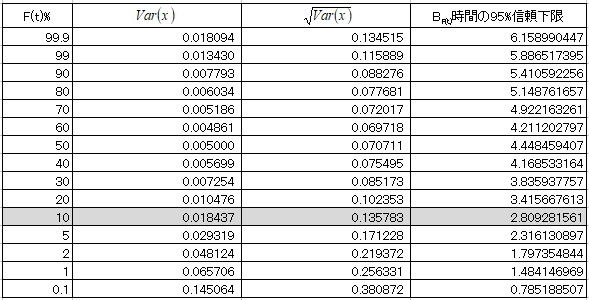
　以上の計算により、Var(x)を推定するためのy 以外の項が求まったことになる。Var(x)を推定するにはy を定義する必要があり、B₁₀ライフの信頼下限を推定する場合のy は以下のようにワイブル関数において不信頼度F(t)=0.1を代入することで得られる。最終的には時間の信頼限界を推定することになり、それにはB₁₀ライフにおけるx の値を推定し、更にx の信頼下限を求めた後で時間に変換することになる。以上を計算すると以下のように計算される。
　　
　x の推定値（1.256293）は、回帰直線とF(t)=10%の交点から上側（直線軸：ln(t)）のX軸の値に相当し、x の信頼下限値（1.032927）も同様に上側のX軸が適用される。最後に時間の観点（つまり下側のX軸：t）で捉えるために最後の式で変換し、B₁₀における時間の信頼下限値として2.809（×10³）万回が得られたことになる。このように手で計算するとかなり面倒ではあるが、EXCELの関数や専用プログラムで計算すれば、非常に簡単に推定することが可能になる。仮にF(t)の値として0.1～99.9%までの範囲で全てを計算すれば、その範囲の連続したカーブのFM信頼限界が得られることになる。これらをチャートに図示すると以下のようになり、0.1～99.9%までの計算結果を下表に示す。回帰分析を経験した人は直ぐに直観できると思うが、信頼性解析ではデータが順序統計量となり仮定する分布もワイブル分布なので、前者と比較すると少し複雑になるのは止むを得まい。



　　
　　

2.2不完全データの解析（試験の途中において中間報告する場合）
1)故障個数が0個の場合
　2.1項が試験終了後の最終報告とするなら、この場合は試験途中における中間報告である。既に何回も記述しているように、信頼性試験では二つの壁があり最終結果を得るまでに非常に時間が掛かる。だからと言って顧客から信頼性データの要求があった際に、「試験継続中で結論が得られていません」との回答では、競合する会社が多くある中何とも頼りない対応であり、土俵に上がるための声を掛けて貰えない可能性もある。そのような際にも具体的な信頼性特性値を示そうというものである。2.1項の信頼性データにおいて、3,000万回時点で中間報告することを考えてみよう。
　試験経過回数（時間）：3000万回
　故障個数：0個
　良品継続個数：8個（3000万回～継続中）
　このような条件で、客観的具体的に何が言えるかである。3000万回試験を実施し故障個数が0個であったから、寿命は「少なくとも3000万回程度はあるだろう」との予測はできるが、あくまでサンプルデータであり勿論言い張ることはできない。そこで言い張るためにはどのように考えればいいかである。理論編の7.3項にあるように故障個数が0個の場合は、ある一定試験経過後の信頼度は片側信頼水準(P_α)と試料数から一義的に決定する。この考え方及び理論編の8項「最短試験規模」における論理展開から、試験時間（t_s）と目標時間（t_p）の比を求めることができる。つまり試験時間から、言い張れる目標時間が推定できるということになる。但し条件が一つあり、過去の同類製品の信頼性試験により形状Par.（m）は既知である必要がある。理論編の展開式より、以下の計算結果が得られる。
　
　目標時間（t_p=B₁₀）における信頼度R(t_p)は0.9、片側信頼水準(P_α=0.9)とすると、試験時間3000万回時点において言い張れる信頼性特性値（B₁₀）は約2450万回程度となり、この値は最終的な解析結果である3400万回に対しかなり控えめな値になる。
2)故障個数が1個以上の場合
　この例として、4000万回経過後に中間報告することを考えよう。
　試験経過回数（時間）：4000万回
　故障個数：c =2個（3450万回、3950万回）
　良品継続個数：6個（4000万回～継続中）
　この場合（c≧1）の信頼度は故障個数が0個の時とは異なり、理論編の9項「ワイブル分布の計数1回抜き取りLTFR（Lot ToleranceFailure Rate）方式」の以下の二項分布の式により、試験経過時間t_sにおける信頼度R(t_s)を求める必要がある。推定確率p_g(y)はn 個の試料数において故障がc 個発生する確率で、未知数はR(t_s)のみとなる。c =0 の場合は理論編7.3項の考え方により手計算が可能であるが、試料数が多い場合はほぼ不可能なためプログラムが得意とする収束計算で求める必要があり、β=0.1（10%）における（n=*,c=*）を計算すると下右表のような値が得られ、（n =8,c =2）ではR(t_s)=0.467が得られている。これらの結果及び理論編の8項展開式からt_pを計算すると、下左表のように求められる。この考え方では、c =0と置いて（n =*,c =0）における信頼度を代入して計算すれば、故障個数が0個の場合にも適用できるので、管理人のプログラムはこの方式を用いて計算している。
　
　　　
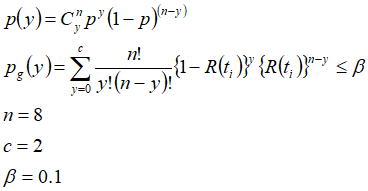
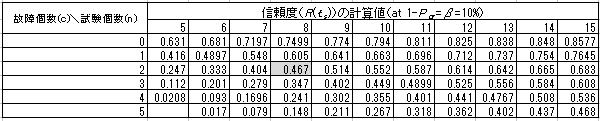
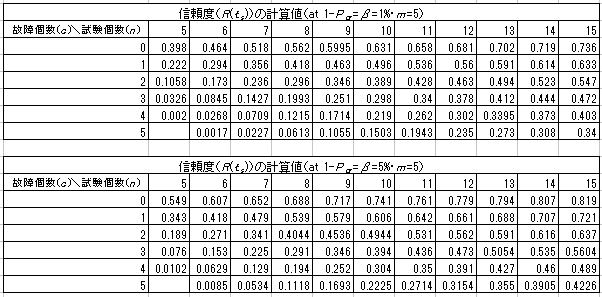
　信頼度R(t_p)0.9の列の試験時間4000万回時点（故障個数2個）における信頼性特性値（B₁₀）は、約2690万回程度と推定された。0個の場合と同様に最終的な解析結果である3400万回に対して控えめな値になるが、これは打ち切り時間における信頼度の推定において、信頼度の下限値を推定しているためである。片側信頼水準（若しくは消費者危険率）と試験個数を変化させた場合の信頼度の下限値は、以下表のように変化する。試験個数を一定とした場合は片側信頼水準が大きい（消費者危険率が小さい）程小さくなり、片側信頼水準を一定とした場合は試料数が多い程大きくなることが分かる。一つ比較例を挙げると、β=10%における（n,c）=（5,0）の信頼度とβ=1%における（n,c）=（10,0）の信頼度は同じ0.631の値を示しており、最短試験規模の割増係数は何れの条件も1.343になる。つまり当初の試験計画として、β=10%に設定して試料数n =5で予定していた試験を、仮にn =10で同じ最短試験規模まで試験を実施した場合β=1%が確保（消費者危険率が下がった）されたことになり、試料数を増大することによりパラメータの推定精度が高くなることが分かる。

　

３．最短試験規模（ワイブル分布の計数1回抜き取りLTFR方式）
　信頼性試験の二つの壁（数と時間）を克服する一つの方法として最短試験規模がある。予めB₁₀の目標値を設定しておき、一定の信頼水準（あるいは危険率）でそれを宣言できる時間に至ったら、故障数0個のまま試験を打ち切るというものである。最短試験規模とはこの際の打ち切り時間のことであるが、基本的な考え方は故障数が0個の場合の解析と全く同様であり、更には一定の試料数で目標値であるかを検査するとの観点から、抜き取り検査（ワイブル分布の計数1回抜き取りLTFR方式）における故障個数が0個の場合にも適用できる。試験時間（t_s）と目標時間（t_p）の比を求め、試験時間をベースに目標時間を推定した訳である。最短試験規模では観点を逆にして、今度は目標時間をベースに試験時間を推定しようというものである。計算の過程を見る限り、観点を逆にしても比を求めるための計算は変わらないことが分かる。以上の考え方による計算結果を以下に示す。
　
　この例ではB₁₀の目標値としてt_p=3000万回を宣言（消費者危険率：β=0.1）できる最短試験規模は、約3700万回程度と推定される。これらの推定条件には試料数（n=8）、ワイブル形状Par.が既知（m=5）なども含まれ、条件が変われば最短試験規模の推定値も変化する。ワイブル分布の計数1回抜き取りLTFR方式では、ある母集団がt_p=3000万回であるかについて試料数8個で試験し、3700万回まで故障数0個で推移したなら合格判断を下すというように考える訳である。以下に一般的な条件（R(t_p)=0.9、β=0.1）における、試験規模を求めるための割増係数を示す。
　
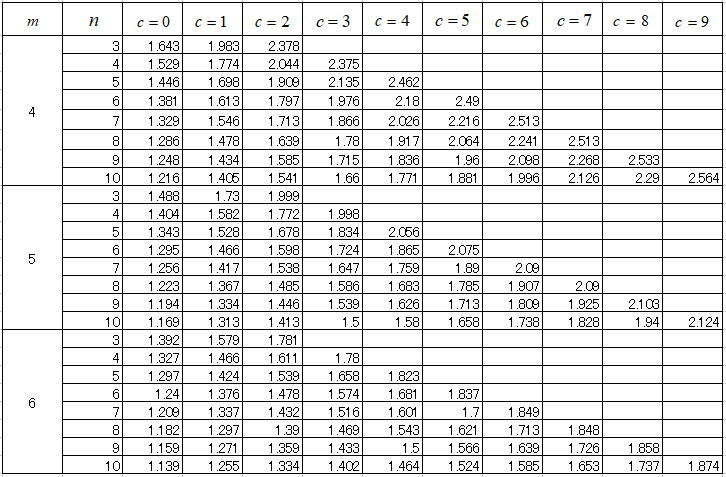
　　上表の係数で故障個数が0個における値が最短試験規模の割増係数となり、割増係数の傾向は以下の通りである。
　1)試料数が少ないと、試験時間は長くなる。
　2)故障分布のばらつきを大きく見積もる（ワイブル形状Par.(m)を小さく見積もる）と、試験時間は長くなる。
　3)故障個数が増大すると、試験時間は長くなる。

３．プログラムによる解析
　ここでは2項で説明した解析例について、管理人が作成した統計解析ツール（SA&RA ProX）による解析結果を示す。このような専用のプログラムを使用すれば、データさえしっかり取得すれば母集団の分布を明確に捉える事が可能になる。
　1)完全データの解析
　管理人のプログラムでは、先ず数値計算解析（最尤法）により母集団のパラメータを推定し、次いでグラフィック解析を実施するよう構成されている。以下に2.1項におけるデータの数値計算解析結果とそれらを纏めた表を示す。
　
　
　
　
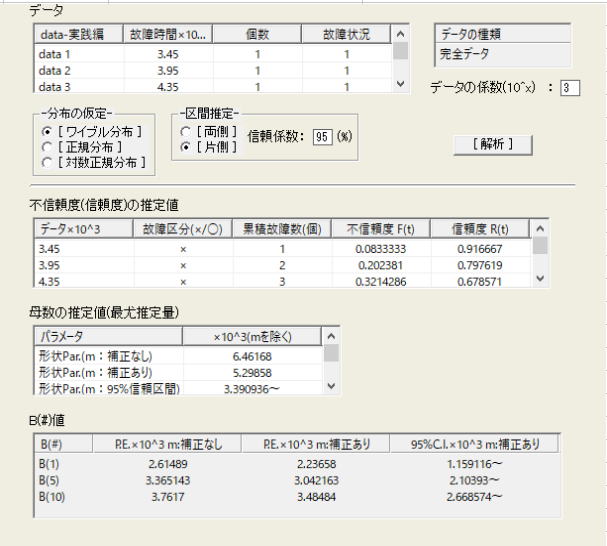
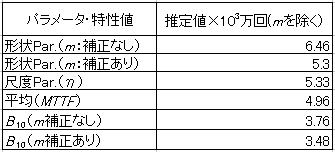
　補正なしとは最尤法による数値計算解析結果そのものの値であり、補正有りは形状Par.の偏りを補正する係数を考慮した値で元の値より若干小さく(回帰直線の傾きとしては大きく)なる。これに伴い信頼性特性値（B₁₀）も小さい方向に補正される。かつてはこのような解析はできなかったが、今やPC上で簡単に解析できるようになったということである。次に同じデータにおけるグラフィック解析結果（MRR-onX,FM（時間））を示す。
　
　　
　
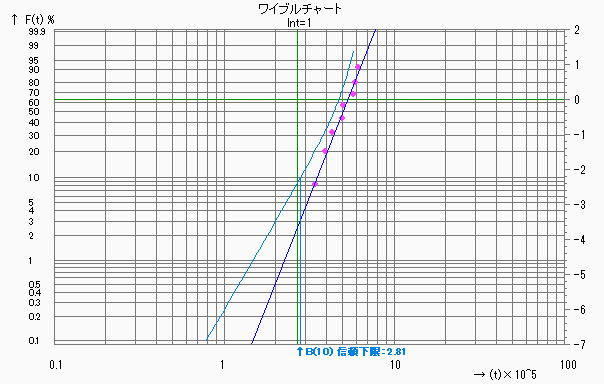
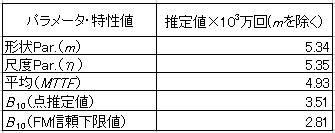
　両者（数値計算解析（最尤法）とグラフィック解析）を比較すると、数値計算解析（最尤法）における補正有りの推定量はグラフィック解析の値とほぼ同じ結果が得られており、我々は一般式を計算するのみであるが数値計算理論の素晴らしさが実感できる。そして2項における手計算による解析結果との比較でも、プログラムのアルゴリズムの関係で表記値より下位の桁では微妙な違いはあるもののほぼ一致しており、何れの手法を用いても正しい結果が得られることが分かる。なおチャートに示してある信頼下限は時間のFM信頼下限を示すものであるが、従来の%ランク点による信頼区間の推定とは異なりF(t_i)のプロット時間領域の外側まで及んでいるため、B₁ライフの信頼下限も十分に読み取れる。%ランク点による区間推定は不信頼度F(t)の区間推定を行うものなので、チャートに示されている信頼限界（時間）とは異なり、FM信頼限界のもう一つの信頼限界（信頼度）に相当するものである。
　2)不完全データの解析
　2.2項と同様な条件でプログラムで解析した結果を示す。前述したようにこのプログラムは、理論編の9項「ワイブル分布の計数1回抜き取りLTFR（Lot ToleranceFailure Rate）方式」に基づくものであり、信頼性特性値を指定し所要の推定アイテム（試験規模、危険率、宣言地）に応じた条件を入力することにより、故障個数の有無に関わらず推定値が得られるものである。
　試験規模：目標時間を宣言できる試験規模を推定
　危険率：目標時間を宣言した場合の危険率を推定
　目標値：一定試験経過後の故障数より宣言できる特性値を推定
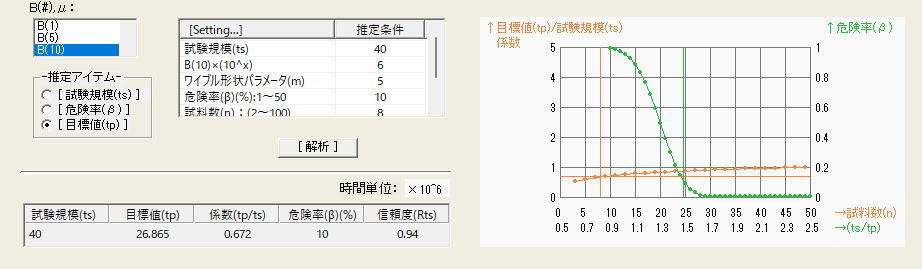
　以下は3000万回試験を実施し、故障個数0個において宣言できる信頼性特性値（B₁₀）を推定したものであり、2項の計算結果と一致している。この結果から一つ分かることがある。2.2-1)項「故障個数が0個の場合」の目標時間(t_p)は片側信頼水準(P_α)90%における計算値であるが、プログラムによる計算値(目標値)は消費者危険率(β)10%における値である。つまり消費者危険率(β)は、(1-P_α)ということになる。グラフ出力にあるように危険率は試験時間の経過に伴い低下するため、試験時間が更に経過すれば同じ目標値（ここでは2450万回）を宣言する場合は10%より小さいβを確保出来る、若しくは同じ危険率（ここでは10%）とするなら、より大きい目標値を宣言できることになる。

　
　
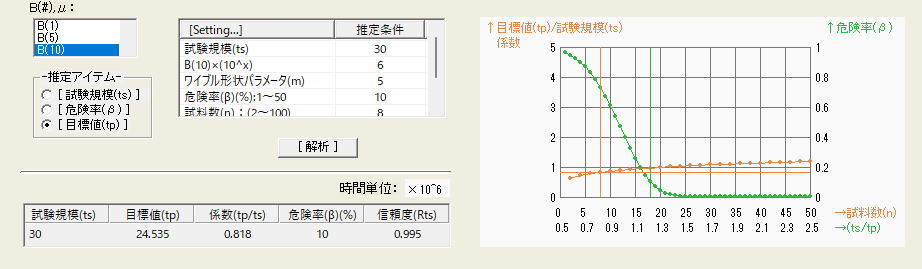
　4000万回まで試験を実施し、故障個数が2個発生した場合の宣言できる信頼性特性値（B₁₀）推定したものであり、2項計算結果とほぼ一致（2項計算結果の2693万回に対し2687万回）している。
　
　
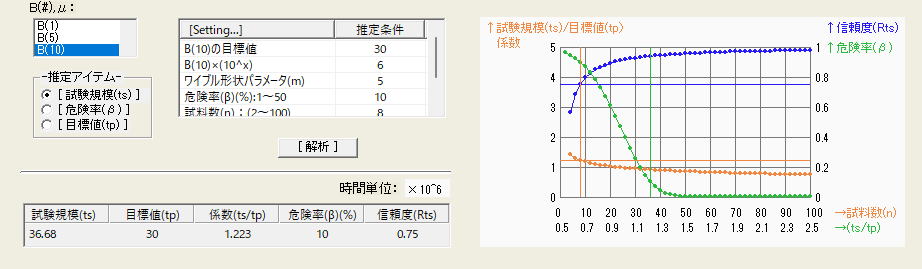
　　目標時間B₁₀=3000万回を危険率10%で宣言できる試験時間を推定したものであり、2項計算結果と一致している。
　
　　　

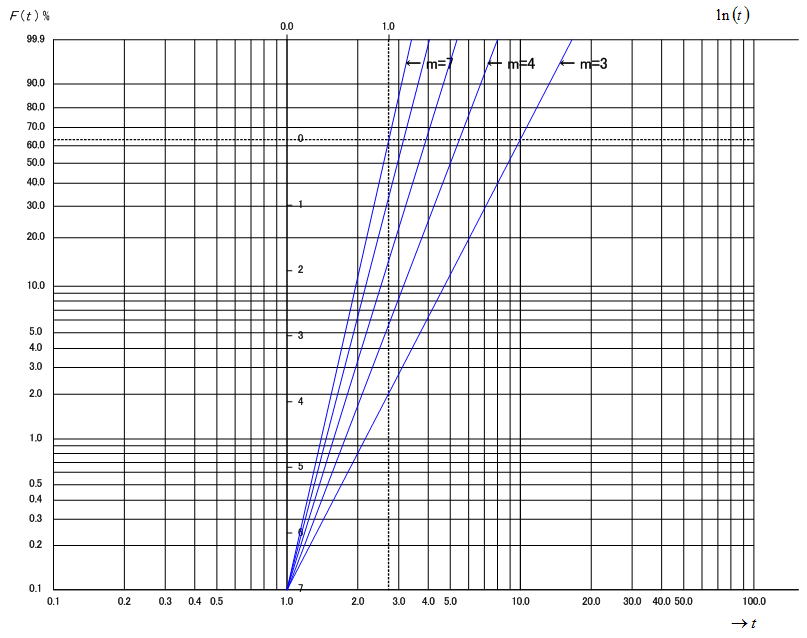
４．纏め
　信頼性解析ではツールに頼らなければならない解析（最尤法、FM信頼限界、故障数がある場合の信頼度の推定）もあるが、2項にあるように特別なツールがなくても十分な解析結果が得られることが分かって頂けたと思う。ここ10年来の大きな動きとして、設備に使用される機器の製造者は確度の高い信頼性データを顧客に提供しなければならなくなっており、エンジニアは少なくとも実践編に記載された解析手法は身に付けて欲しいものである。また折角多くの時間を掛けて試験を実施したのに、データ解析を中途半端にすることは要素データの蓄積の観点からも大きな損失であり、是非実践編の内容を参考に解析して頂くことを望む。最後に信頼性のばらつきについて少し触れておこう。エンジニアはコストバランスを考慮した上で、出来る限り製品の機能特性や信頼性（耐久性）がばらつかないよう設計する訳であるが、信頼性試験を実施すると信頼性が意外な程ばらつく事が往々にしてある。下図はワイブル形状Par.がm=3～m=7の回帰直線の不信頼度0.1%における時間を、同じ時間にした場合の不信頼度の99.9%到達時間を示したものであるが、例えば形状Par.m=4の分布について言えば約8倍の範囲にばらつくことが分かる。この程度のばらつき具合は、信頼性試験においては珍しいことではなくごく普通に見られるばらつきである。つまり設計検討を十分重ねて機能特性がばらつかないよう設計しても、信頼性は意外にばらつく要素があることになる。製品を改良（リフレッシュ）するテーマなどでは、機能特性の改良やコストダウンばかりに目が向く傾向があるが、是非信頼性のばらつきについても因子解明のメスを入れて頂き、形状Par.の値が1～2以上UPさせられるよう検討されたい。